正五角形の不思議

図形と数って、凡人にはわからない神秘の世界って感じがしませんか？
例えば１，１とやって前の二つの数字を足した数を次に書くと、
１，１，２、３、５、８、１３、２１・・・
ってなっていく。有名なフィボナッチの数列だけど、これのｎ番目と
ｎ引く１番目の比は黄金比ってやつになるんですよね。
ピタゴラスの定理も不思議といえば不思議。
ａの2乗をa^2と書くとして、直角三角形は
a^2 ＋ b^2 = c^2
なんかきれいすぎてだまされた気分にならない？

さて正五角形、360度を5等分にすると72度なんて変な数だし、
五角形の辺と辺の間の角度は108度（3/5π）だし、
分度器を使って書いても書きにくいよね。

これのシンプルな作図方法を書きます。




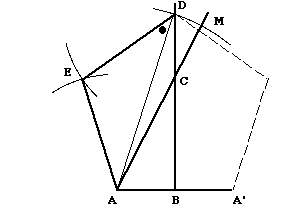
具体的に数字で書くことにします。AA'が２、その中点をBとするとABが１、
Bから垂直な線BCをのばし、AA'分だけ行った所（２ですね）をCとすると、
ACは��5になりますネ。
ACを伸ばしてCからAB分だけ（１です）行ったところの点をMとすると
AMは��5＋１、
Aを中心にしてAMを半径にした弧を書いて、BCの線と交わる点をDとすると
正五角形の頂点になります。おや、もう出来た！
あとは、Dから半径AA'（２です）の弧を書いて、Aからも書いて交わった点が
Eになって、それぞれを結べば五角形の片割れができました。

正五角形の角DEAは 3/5πだから、角ADE（黒丸のところ）は 1/5π
です。（2等辺三角形だからね）
cos1/5πは ADの半分 割る ED
（点EからADに垂線を下せば、2等辺三角形の垂線は中点を通るからネ）
（��5＋１）/２　割る　２は・・・
はい、1/4（��5＋１）になりました。

図を書く時は別にルートなんて気にしないで線を引いたり
円をかいたりするだけだし、意外に簡単です。

そして、正五角形の一辺の長さと対角線の比・・AA'とADの比は
２：��5＋１ですが、これが黄金比なんですよね。。
なんだか不思議。



この日の更新の記録を見てみる

みーはーに戻る

ホームへ戻る